常见密码算法总结
有这个想法大概是在看校赛复赛逆向writeup的时候,第三题是一道用了改动过的md5,学长在writeup时候说,最好要对常见的加密算法的特征有一个了解。然后在去年打湖湘杯初赛的时候,因为有好几道题都跟密码学算法有关,于是又想起了这个想法…….结果可耻地拖到现在TMD,算是上学期的一个坑吧,希望给我的填坑之旅开个好头。
MD5
果然是不可能有好的开头的……到网上去找md5的源码想看一看,发现有好多不同的版本NMD。不过一般来讲都有以下三个函数:
1 | MD5Init(&md5); |
MD5Init函数中有MD5算法的一个非常明显的特征:在该函数内,会对4个32比特的寄存器进行初始化,初始化值如下
1 | void MD5_Init(MD5_CTX *ctx) |
往往还有会有一个名叫transform的函数(内容差不多),该函数内主要是分块后循环处理时的函数,很多很多行,如下
1 | MD5Transform(buf, inraw) |
md5伪代码如下(来自wiki):
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
>var int[64] r, k
>
>//r specifies the per-round shift amounts
>r[ 0..15]:= {7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22}
>r[16..31]:= {5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20}
>r[32..47]:= {4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23}
>r[48..63]:= {6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21}
>
>//Use binary integer part of the sines of integers as constants:
>for i from 0 to 63
> k[i] := floor(abs(sin(i + 1)) × 2^32)
>
>//Initialize variables:
>var int h0 := 0x67452301
>var int h1 := 0xEFCDAB89
>var int h2 := 0x98BADCFE
>var int h3 := 0x10325476
>
>//Pre-processing:
>append "1" bit to message
>append "0" bits until message length in bits ≡ 448 (mod 512)
>append bit length of message as 64-bit little-endian integer to message
>
>//Process the message in successive 512-bit chunks:
>for each 512-bit chunk of message
> break chunk into sixteen 32-bit little-endian words w[i], 0 ≤ i ≤ 15
>
> //Initialize hash value for this chunk:
> var int a := h0
> var int b := h1
> var int c := h2
> var int d := h3
>
> //Main loop:
> for i from 0 to 63
> if 0 ≤ i ≤ 15 then
> f := (b and c) or ((not b) and d)
> g := i
> else if 16 ≤ i ≤ 31
> f := (d and b) or ((not d) and c)
> g := (5×i + 1) mod 16
> else if 32 ≤ i ≤ 47
> f := b xor c xor d
> g := (3×i + 5) mod 16
> else if 48 ≤ i ≤ 63
> f := c xor (b or (not d))
> g := (7×i) mod 16
>
> temp := d
> d := c
> c := b
> b := leftrotate((a + f + k[i] + w[g]),r[i]) + b
> a := temp
> Next i
> //Add this chunk's hash to result so far:
> h0 := h0 + a
> h1 := h1 + b
> h2 := h2 + c
> h3 := h3 + d
>End ForEach
>var int digest := h0 append h1 append h2 append h3 //(expressed as little-endian)
>
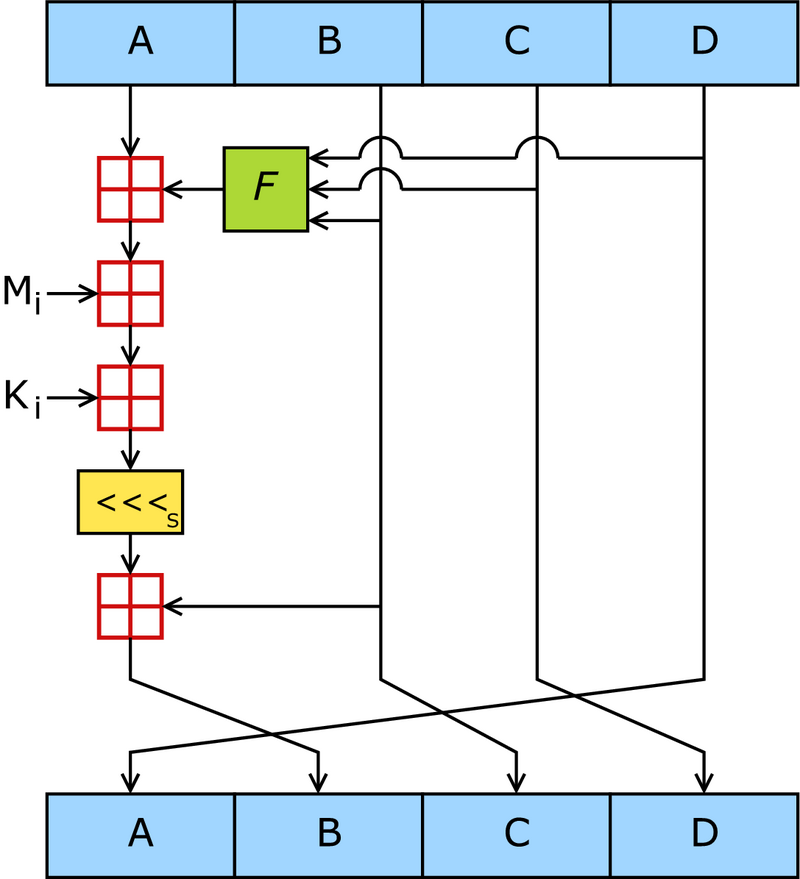
一个MD5运算由类似的64次循环构成(如下图),分成4组16次。F:一个非线性函数;一个函数运算一次。Mi:表示一个 32-bits 的输入数据,Ki:表示一个 32-bits 常数,用来完成每次不同的计算。
本来只准备简单写一下……但是找到了一篇博客,而且复赛那道题的源码应该是就是在这个版本的源码上改动的,究极舒适.jpg。这篇博客写得非常详细,直接看博客好了。
https://blog.csdn.net/ZCShouCSDN/article/details/83866095
SHA-1
在看md5、sha-1、sha-2的时候发现这几类哈希函数大致的处理过程都是差不多的,比如说都要先做填充、附加、初始化寄存器,分块处理、会有一个结构体来储存相关信息等等。
1 | typedef struct |
无论是md5、还是sha-1、sha-2中都会有一个结构体,储存的信息也都差不多。
sha-1在刚开始会初始化5个32位的寄存器,比md5多一个,在这里也可已看出sha-1的最终摘要长度为160位:
1 | void SHA1Init(SHA1_CTX *context) |
sha-1伪代码如下(来自Wiki):
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
>//Initial variables:
> h0 := 0x67452301
> h1 := 0xEFCDAB89
> h2 := 0x98BADCFE
> h3 := 0x10325476
> h4 := 0xC3D2E1F0
>//Pre-processing:
>append the bit '1' to the message
>append k bits '0', where k is the minimum number >= 0 such that the resulting message
> length (in bits) is congruent to 448(mod 512)
>append length of message (before pre-processing), in bits, as 64-bit big-endian integer
>//Process the message in successive 512-bit chunks:
>break message into 512-bit chunks
>for each chunk
> break chunk into sixteen 32-bit big-endian words w[i], 0 ≤ i ≤ 15
>//Extend the sixteen 32-bit words into eighty 32-bit words:
>for i from 16 to 79
> w[i] := (w[i-3] xor w[i-8] xor w[i-14] xor w[i-16]) leftrotate 1
>//Initialize hash value for this chunk:
> a := h0
> b := h1
> c := h2
> d := h3
> e := h4
>//Main loop:
>for i from 0 to 79
> if 0 ≤ i ≤ 19 then
> f := (b and c) or ((not b) and d)
> k := 0x5A827999
> else if 20 ≤ i ≤ 39
> f := b xor c xor d
> k := 0x6ED9EBA1
> else if 40 ≤ i ≤ 59
> f := (b and c) or (b and d) or(c and d)
> k := 0x8F1BBCDC
> else if 60 ≤ i ≤ 79
> f := b xor c xor d
> k := 0xCA62C1D6
> temp := (a leftrotate 5) + f + e + k + w[i]
> e := d
> d := c
> c := b leftrotate 30
> b := a
> a := temp
>//Add this chunk's hash to result so far:
> h0 := h0 + a
> h1 := h1 + b
> h2 := h2 + c
> h3 := h3 + d
> h4 := h4 + e
>//Produce the final hash value (big-endian):
>digest = hash = h0 append h1 append h2 append h3 append h4
>
上述关于
f表达式列于FIPS PUB 180-1中,以下替代表达式也许也能在主要循环里计算f:
2
3
4
5
6
>
>(40 ≤ i ≤ 59): f := (b and c) or (d and (b or c)) (alternative 1)
>(40 ≤ i ≤ 59): f := (b and c) or (d and (b xor c)) (alternative 2)
>(40 ≤ i ≤ 59): f := (b and c) + (d and (b xor c)) (alternative 3)
>
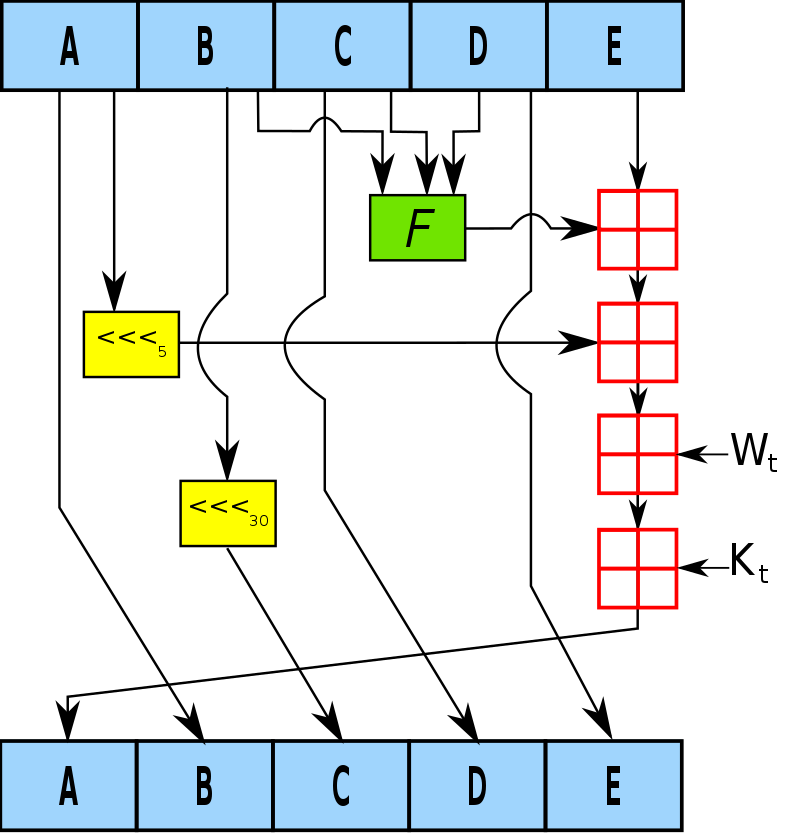
SHA-1压缩算法中的一个循环如下图所示。A, B, C, D和E是这个state中的32位文字;F是会变化的非线性函数;<<<n代表bit向左循环移动n个位置。n因操作而异。田代表modulo 232之下的加法,Kt是一个常量。
emmmmm感觉好像没什么写的了orz….
找到了一篇很好的博客,算了直接放地址吧…..
https://blog.csdn.net/ZCShouCSDN/article/details/83866095
和写md5那篇博客是同一个作者
SHA-256
由于sha-1的不安全性,所以就有了sha-2系列。sha-256是sha-2算法的一种,因其消息摘要长度为256位而得名,与sha-224、sha-384、sha-512等同属一个系列,不同如下
SHA-224和SHA-256基本上是相同的,除了:
h0到h7的初始值不同,以及- SHA-224输出时截掉
h7的函数值。SHA-512和SHA-256的结构相同,但:
- SHA-512所有的数字都是64位,
- SHA-512运行80次加密循环而非64次,
- SHA-512初始值和常量拉长成64位,以及
- 二者比特的偏移量和循环位移量不同。
SHA-384和SHA-512基本上是相同的,除了:
h0到h7的初始值不同,以及- SHA-384输出时截掉
h6和h7的函数值。
以上来自Wiki,h0、h6和h7为初始化寄存器。
sha-2系列会初始化8个32位的寄存器(sha-512是8个64位的寄存器),这好像是所有哈希函数的主要特征…..
1 | void sha256_init(SHA256_CTX *ctx) |
sha-256伪代码(来自wiki):
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
>//Initialize variables
>(first 32 bits of the fractional parts of the square roots of the first 8 primes 2..19):
> h0 := 0x6a09e667
> h1 := 0xbb67ae85
> h2 := 0x3c6ef372
> h3 := 0xa54ff53a
> h4 := 0x510e527f
> h5 := 0x9b05688c
> h6 := 0x1f83d9ab
> h7 := 0x5be0cd19
>//Initialize table of round constants
>(first 32 bits of the fractional parts of the cube roots of the first 64 primes 2..311):
>k[0..63] :=
> 0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5,
> 0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3, 0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174,
> 0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc, 0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da,
> 0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7, 0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967,
> 0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13, 0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85,
> 0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070,
> 0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3,
> 0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208, 0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2
>//Pre-processing:
>append the bit '1' to the message
>append k bits '0', where k is the minimum number >= 0 such that the resulting message
> length (in bits) is congruent to 448(mod 512)
>append length of message (before pre-processing), in bits, as 64-bit big-endian integer
>//Process the message in successive 512-bit chunks:
>break message into 512-bit chunks
>for each chunk
> break chunk into sixteen 32-bit big-endian words w[0..15]
>//Extend the sixteen 32-bit words into sixty-four 32-bit words:
> for i from 16 to 63
> s0 := (w[i-15] rightrotate 7) xor (w[i-15] rightrotate 18) xor(w[i-15] rightshift 3)
> s1 := (w[i-2] rightrotate 17) xor (w[i-2] rightrotate 19) xor(w[i-2] rightshift 10)
> w[i] := w[i-16] + s0 + w[i-7] + s1
>//Initialize hash value for this chunk:
> a := h0
> b := h1
> c := h2
> d := h3
> e := h4
> f := h5
> g := h6
> h := h7
>//Main loop:
>for i from 0 to 63
> s0 := (a rightrotate 2) xor (a rightrotate 13) xor(a rightrotate 22)
> maj := (a and b) xor (a and c) xor(b and c)
> t2 := s0 + maj
> s1 := (e rightrotate 6) xor (e rightrotate 11) xor(e rightrotate 25)
> ch := (e and f) xor ((not e) and g)
> t1 := h + s1 + ch + k[i] + w[i]
> h := g
> g := f
> f := e
> e := d + t1
> d := c
> c := b
> b := a
> a := t1 + t2
>//Add this chunk's hash to result so far:
> h0 := h0 + a
> h1 := h1 + b
> h2 := h2 + c
> h3 := h3 + d
> h4 := h4 + e
> h5 := h5 + f
> h6 := h6 + g
> h7 := h7 + h
>//Produce the final hash value (big-endian):
>digest = hash = h0 append h1 append h2 append h3 append h4 append h5 append h6 append h7
>
SHA-2的第t个加密循环如下图所示。图中的深蓝色方块是事先定义好的非线性函数。ABCDEFGH一开始分别是八个初始值,Kt是第t个密钥,Wt是本区块产生第t个word。原消息被切成固定长度的区块,对每一个区块,产生n个word(n视算法而定),透过重复运作循环n次对ABCDEFGH这八个工作区块循环加密。最后一次循环所产生的八段字符串合起来即是此区块对应到的散列字符串。若原消息包含数个区块,则最后还要将这些区块产生的散列字符串加以混合才能产生最后的散列字符串。

AES
直接放两篇博客算了……这两篇写得很清楚明了。
https://github.com/matt-wu/AES
https://blog.csdn.net/qq_28205153/article/details/55798628
算了还是瞎jb写点东西吧,aes算法一个重要的特征就是有一个S盒,以及初始密钥。比如2018年湖湘杯的一题

很容易可以看出byte_7FF62DD6DA40是初始密钥,点进byte_7FF62DD6AC50可以看到这是一个s盒

所以可以判断出这个算法的基础是aes算法。
DES
des是一个非常经典的对称加密算法,不过用于其安全性现在已经很少使用了。
des的核心思想是混淆和扩散,看源码的时候会发现它在不停地做置换,同时也会看到定义了很多表。
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
> int IP[] = { 58, 50, 42, 34, 26, 18, 10, 2,
> 60, 52, 44, 36, 28, 20, 12, 4,
> 62, 54, 46, 38, 30, 22, 14, 6,
> 64, 56, 48, 40, 32, 24, 16, 8,
> 57, 49, 41, 33, 25, 17, 9, 1,
> 59, 51, 43, 35, 27, 19, 11, 3,
> 61, 53, 45, 37, 29, 21, 13, 5,
> 63, 55, 47, 39, 31, 23, 15, 7 };
>
> // 结尾置换表
> int IP_1[] = { 40, 8, 48, 16, 56, 24, 64, 32,
> 39, 7, 47, 15, 55, 23, 63, 31,
> 38, 6, 46, 14, 54, 22, 62, 30,
> 37, 5, 45, 13, 53, 21, 61, 29,
> 36, 4, 44, 12, 52, 20, 60, 28,
> 35, 3, 43, 11, 51, 19, 59, 27,
> 34, 2, 42, 10, 50, 18, 58, 26,
> 33, 1, 41, 9, 49, 17, 57, 25 };
>
> /*------------------下面是生成密钥所用表-----------------*/
>
> // 密钥置换表,将64位密钥变成56位
> int PC_1[] = { 57, 49, 41, 33, 25, 17, 9,
> 1, 58, 50, 42, 34, 26, 18,
> 10, 2, 59, 51, 43, 35, 27,
> 19, 11, 3, 60, 52, 44, 36,
> 63, 55, 47, 39, 31, 23, 15,
> 7, 62, 54, 46, 38, 30, 22,
> 14, 6, 61, 53, 45, 37, 29,
> 21, 13, 5, 28, 20, 12, 4 };
>
> // 压缩置换,将56位密钥压缩成48位子密钥
> int PC_2[] = { 14, 17, 11, 24, 1, 5,
> 3, 28, 15, 6, 21, 10,
> 23, 19, 12, 4, 26, 8,
> 16, 7, 27, 20, 13, 2,
> 41, 52, 31, 37, 47, 55,
> 30, 40, 51, 45, 33, 48,
> 44, 49, 39, 56, 34, 53,
> 46, 42, 50, 36, 29, 32 };
>
> // 每轮左移的位数
> int shiftBits[] = { 1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1 };
>
> /*------------------下面是密码函数 f 所用表-----------------*/
>
> // 扩展置换表,将 32位 扩展至 48位
> int E[] = { 32, 1, 2, 3, 4, 5,
> 4, 5, 6, 7, 8, 9,
> 8, 9, 10, 11, 12, 13,
> 12, 13, 14, 15, 16, 17,
> 16, 17, 18, 19, 20, 21,
> 20, 21, 22, 23, 24, 25,
> 24, 25, 26, 27, 28, 29,
> 28, 29, 30, 31, 32, 1 };
>
> // S盒,每个S盒是4x16的置换表,6位 -> 4位
> int S_BOX[8][4][16] = {
> {
> { 14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7 },
> { 0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8 },
> { 4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0 },
> { 15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13 }
> },
> {
> { 15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10 },
> { 3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5 },
> { 0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15 },
> { 13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9 }
> },
> {
> { 10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8 },
> { 13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1 },
> { 13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7 },
> { 1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12 }
> },
> {
> { 7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15 },
> { 13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9 },
> { 10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4 },
> { 3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14 }
> },
> {
> { 2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9 },
> { 14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6 },
> { 4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14 },
> { 11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3 }
> },
> {
> { 12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11 },
> { 10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8 },
> { 9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6 },
> { 4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13 }
> },
> {
> { 4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1 },
> { 13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6 },
> { 1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2 },
> { 6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12 }
> },
> {
> { 13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7 },
> { 1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2 },
> { 7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8 },
> { 2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11 }
> }
> };
>
> // P置换,32位 -> 32位
> int P[] = { 16, 7, 20, 21,
> 29, 12, 28, 17,
> 1, 15, 23, 26,
> 5, 18, 31, 10,
> 2, 8, 24, 14,
> 32, 27, 3, 9,
> 19, 13, 30, 6,
> 22, 11, 4, 25 };
>
>
>
过程还是看书上的吧,书上比网上的博客说的好。
IDEA
一种比较新的对称加密算法,分组长度为64位,密钥长度为128位。
在加密时64位的明文会被分成4个16位的分组,在接下来的8轮运算中与6个16的密钥进行运算。密钥的产生主要是通过密钥环移来实现的。
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
> * @brief Encrypt a 16-byte block using IDEA algorithm
> * @param[in] context Pointer to the IDEA context
> * @param[in] input Plaintext block to encrypt
> * @param[out] output Ciphertext block resulting from encryption
> **/
>
> void ideaEncryptBlock(IdeaContext *context, const uint8_t *input, uint8_t *output)
> {
> uint_t i;
> uint16_t e;
> uint16_t f;
> uint16_t *k;
>
> //The plaintext is divided into four 16-bit registers
> uint16_t a = LOAD16BE(input + 0);
> uint16_t b = LOAD16BE(input + 2);
> uint16_t c = LOAD16BE(input + 4);
> uint16_t d = LOAD16BE(input + 6);
>
> //Point to the key schedule
> k = context->ek;
>
> //The process consists of eight identical encryption steps
> for(i = 0; i < 8; i++)
> {
> //Apply a round
> a = ideaMul(a, k[0]);
> b += k[1];
> c += k[2];
> d = ideaMul(d, k[3]);
>
> e = a ^ c;
> f = b ^ d;
>
> e = ideaMul(e, k[4]);
> f += e;
> f = ideaMul(f, k[5]);
> e += f;
>
> a ^= f;
> d ^= e;
> e ^= b;
> f ^= c;
>
> b = f;
> c = e;
>
> //Advance current location in key schedule
> k += 6;
> }
>
> //The four 16-bit values produced at the end of the 8th encryption
> //round are combined with the last four of the 52 key sub-blocks
> a = ideaMul(a, k[0]);
> c += k[1];
> b += k[2];
> d = ideaMul(d, k[3]);
>
> //The resulting value is the ciphertext
> STORE16BE(a, output + 0);
> STORE16BE(c, output + 2);
> STORE16BE(b, output + 4);
> STORE16BE(d, output + 6);
> }
>
如上为主要的8轮循环加密。运算主要是异或,模2的16次方加,模2的16次方+1乘。
RC4
一种经典的流密码,主要通过一个s盒对明文进行加密,已被破解。
看源码的时候发现这大概是我看过的最简单的密码算法源码了。
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
>{
> int i, j;
> BYTE t;
>
> for (i = 0; i < 256; ++i)
> state[i] = i;
> for (i = 0, j = 0; i < 256; ++i) {
> j = (j + state[i] + key[i % len]) % 256;
> t = state[i];
> state[i] = state[j];
> state[j] = t;
> }
>}
>
>// This does not hold state between calls. It always generates the
>// stream starting from the first output byte.
>void arcfour_generate_stream(BYTE state[], BYTE out[], size_t len)
>{
> int i, j;
> size_t idx;
> BYTE t;
>
> for (idx = 0, i = 0, j = 0; idx < len; ++idx) {
> i = (i + 1) % 256;
> j = (j + state[i]) % 256;
> t = state[i];
> state[i] = state[j];
> state[j] = t;
> out[idx] = state[(state[i] + state[j]) % 256];
> }
>}
>
第一个函数为初始化s盒的函数,第二个即为加密生成密文流的函数。
国密系列
老实说还是因为写这篇总结才会去翻一翻国密系列的算法,这个系列的算法都是比较新的算法,当时段段也没有讲,网上的资料也蛮少的(连个流程图都找不到)。
国密即国家密码局认定的国产密码算法,主要有SM1、SM2、SM3、SM4。
SM1为对称加密,加密算法不公开。
SM2为非对称加密,基于ECC。
SM3为消息摘要。
SM4为分组对称加密。
emmm主要还是看了看SM4吧。
一篇博客,关于SM4的。
https://blog.csdn.net/cg129054036/article/details/83012721
然后是知乎上一个作者写的一系列的文章,SM2、SM3、SM4都介绍得还可以。
https://www.zhihu.com/people/diao-si-pao-niu-bu-kao-ji-zhu/posts
参考资料
感觉自己全程化身博客搬运工……算了就当复习密码学了
https://github.com/B-Con/crypto-algorithms
一个算法源码的库,都是一些比较常见的算法。
https://tls.mbed.org/source-code
https://www.oryx-embedded.com/doc/files.html
这些是我看源码的时候主要用到的网站。